编者按：

　　各位粉丝朋友们，欢迎阅读本期小编推送的《汽车驱动桥螺旋锥齿轮齿面测量误差补偿方法》文章。文章主要介绍了提升汽车驱动桥螺旋锥齿轮齿面加工质量对整车的安全与节能性能有重要意义。

　　该文针对汽车驱动桥螺旋锥齿轮实测和理论齿面存在的测量误差，提出了一种基于对偶四元数优化的迭代最近点(ICP)齿面测量误差补偿方法。

　　本篇文章因篇幅较长，特安排两期推送，本期推出文章最后剩余内容。

　　本期推出：汽车驱动桥螺旋锥齿轮齿面测量误差补偿方法(二)

　　4实测结果与分析

　　为了验证本文算法的补偿效果，使用如图6所示HyB-35型齿轮测量机对汽车驱动桥螺旋锥齿轮齿面进行点接触式测量。

 

　　螺旋锥齿轮齿面方程是超越非线性方程，为了让测量结果尽可能全面地反映实测齿面的形貌信息，对螺旋锥齿轮的齿面进行测量时，通常在轴截面上进行网格规划。根据螺旋锥齿轮的齿面构造和螺旋线走向， 保证检测路径最短且不发生碰撞，本文将小齿轮凹齿面进行网格化，划分为5×7=35个点，由背锥向顶锥进行“ S”形测量方式获得齿面测量点数据，如图7所示。

　　根据图7确定的测量路径对螺旋锥齿轮齿面进行测量，获得实测点齿面坐标点集Q。在MATLAB2020软件中绘制理论测量点集P与实际测量点集Q的空间散点图如图8所示。由于误差较小，在三维坐标下看不到全齿面的对应关系，将其局部对应点进行放大展示。其中空心点代表理论测量点，实心点代表实际测量点。

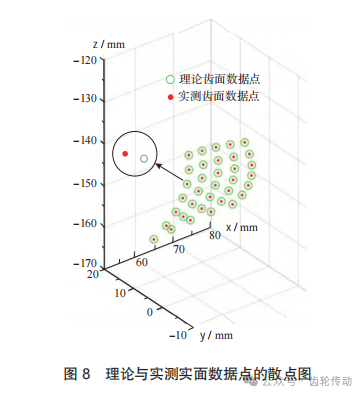
　　本实验点云规模小，在该模型中采用定向对应点， 引入权重系数k，可以有效避免错误对应点的产生。利用本文提出的基于对偶四元数优化的ICP迭代算法误差补偿模型对上述齿面实测数据与理论数据之间的偏差进行补偿，将得到的结果分别与基于SVD分解法、四元数法和L-M法的粗配准结果进行对比，并以对应点间欧氏距离作为评定标准。由实测数据计算出初始平均误差为10.34μm，初始平均误差最大误差为22.11μm，然后对各算法误差补偿效果进行评估。 各算法的粗配准结果如图9所示，由图可知，4种算法经过粗配准后都更靠近零刻线，且SVD法和四元数法进行粗配准的误差补偿效果相差不大，L-M法的x轴方向补偿后误差值与理想坐标偏离较大，本文算法补偿后坐标值与理想坐标值之差与其他3种算法相比更靠近零刻线。证明在粗配准阶段本文算法补偿效果为4种算法中最佳。

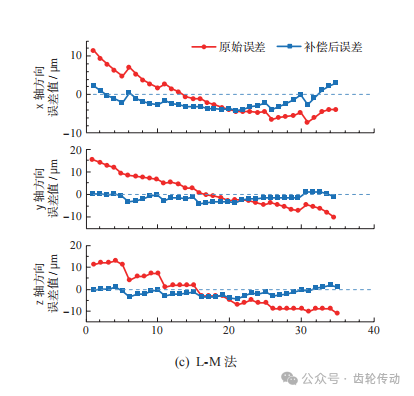
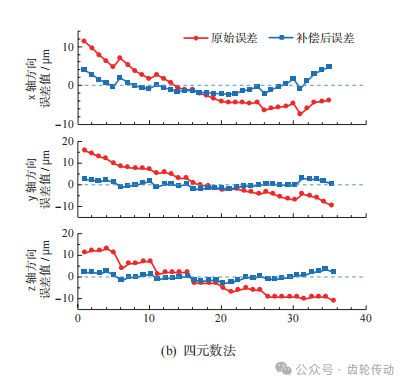
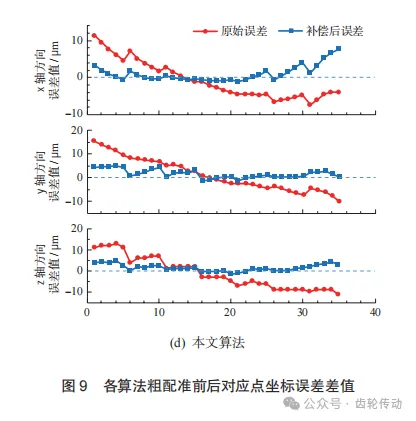
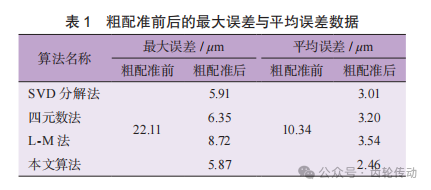
　　表1为粗配准前后的最大误差与平均误差数据。由表可知，4种算法的最大误差分别降低了16.20、15.76、13.39和16.24μm，平均误差分别降低了7.33、7.14、 6.80和7.88μm，本文算法相比于其他算法的结果更优。

　　在粗配准之后，将各算法获取的配准参数值作为精配准的初始参数值。利用点到点 (point-to-point) ICP迭代算法进行精配准，各算法模型中权重k分别等于40%、70%和90%时的补偿效果如图10所示。由图可知，在实验的3组不同权重中，各类算法权重系数k=70%时误差补偿效果最佳，k=90%时次之，k=40%时较差。虽然SVD法、四元数法和L-M法对齿面误差均有补偿作用，但本文算法最终的补偿效果更好，且最终误差更小。

　　精配准后，将基于SVD法、四元数法、L-M法和本文算法进行配准的ICP迭代法的最终误差补偿结果进行分析，根据式(18)给出了各算法模型权重分别为40%、70%和90%时的误差补偿数据结果，并得出各算法10次独立运算时间的均值，如表2所示。由表可得，各算法在权重k为70%时，补偿效果最佳，且本文算法相较于SVD法、四元数法和L-M法进行ICP迭代补偿后的最高误差补偿率分别提升了3.09%、3.10%和3.12%。权重k为70%时，在粗配准阶段，SVD 法、 四元数法、L-M法和本文算法的最大误差由补偿前的22.11μm分别补偿至 5.90、6.35、8.72 和5.87μm，再进一步进行精配准补偿至5.67、5.79、6.38和5.64μm，测量齿面与理论齿面对应点平均误差从10.34μm分别补偿至2.71、2.70、2.70和2.38μm;本文算法相比于其他3种算法平均耗时增加了0.14、0.08和0.18s， 这是由于运行算法的过程中需要调用工具箱Sedumi求解。

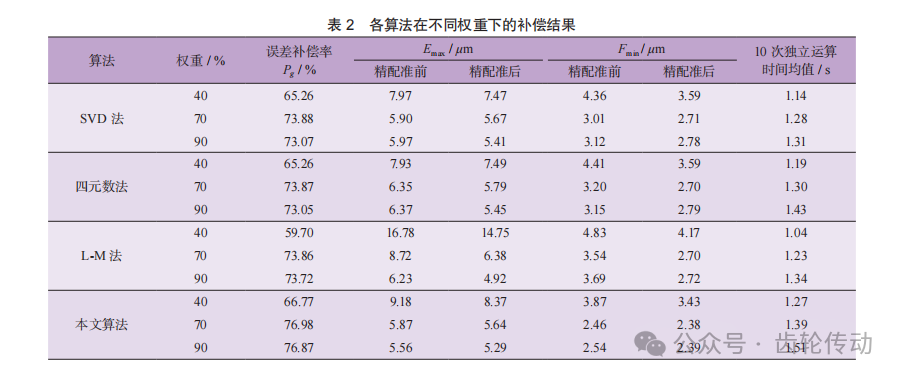
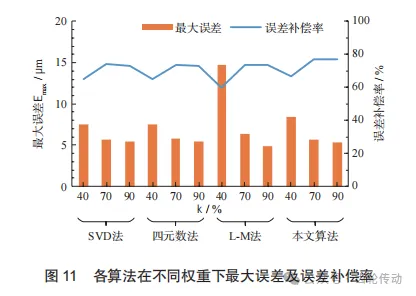
　　如图11所示，将各算法在不同权重下的最终结果进行比较。由图可知，各算法在权重为40%时，最大误差及误差补偿率都较差，这是由于在权重为40%时， 选取的点不足以显示全齿面的数据特征，导致一些齿面点的误差不能进行精细的补偿。而在权重为70%和90%时，各算法的最大误差及误差补偿率相差不大，但70%更佳，这是由于在权重为90%时，虽然几乎包含了所有的齿面数据点，但是不能避免错误对应点的产生，导致最终结果稍有偏移;而在权重为70%时， 有效避免了错误对应点的产生，使齿面测量数据补偿结果更精准。

　　为比较最优权重下各算法对应点的误差补偿效果， 将各算法的全部齿面测量点的误差补偿率绘出，如图12所示。由图可得，4种算法整体趋势大致相同， 且第15—第18点的误差补偿率都偏低，这是由于第15—第18点的原始误差(图9)本身比较小，随着齿面整体旋转配准，此处误差呈现出放大现象。本文算法与其他3种算法相比起伏较小，且整体误差补偿率较高，证明了本文算法相比于其他3种算法有更高的求解精度。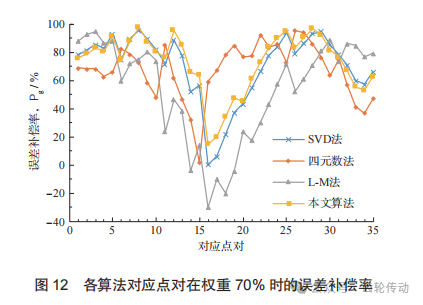

　　为了进一步比较各算法在最优权重下的补偿效果，将各算法在权重70%时最终补偿后的的平均误差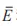和方差s2E计算出，如表3所示。由表可得，本文算法在权重70%补偿后的平均误差 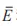为2.392μm，方差s2E为0.147，皆小于其他算法。

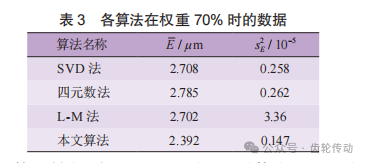
　　综上所述，相比于SVD法、四元数法和L-M法，本文算法在实际测量中求解精度高、稳定性好，验证了其在实际应用中的可行性与有效性。

　　5结论

　　为提升汽车的安全与节能性能，本文针对汽车驱动桥螺旋锥齿轮实测齿面和理论齿面存在的测量误差， 提出了一种基于对偶四元数优化的迭代最近点 (ICP) 齿面测量误差补偿法，利用对偶四元数对齿面配准模型进行表示并使用凸松弛的全局优化算法对旋转矩阵进行优化。由螺旋锥齿轮实际测量实验结果可知，齿轮凹齿面的误差补偿率达77%，最大误差由补偿前的22.11μm降至5.64μm，平均误差由补偿前的10.34μm降至2.38μm。相比于传统奇异值分解法(SVD)、四元数法和Levenberg-Marquardt(L-M)法，本文算法补偿精度和稳定性更高，验证了所提补偿方法的可行性。

　　参考文献略.