针对现有的S型齿廓修形方法存在的问题，设计了一种新的齿廓曲线设计方法。该方法通过使用啮合矩阵实现共轭点的快速求解，并基于共轭点对齿廓曲线进行修形。计算结果表明，改进法设计下的齿廓相比于传统S型齿廓具有更小、更均匀的侧隙，啮合区间得到增大，传动误差有所降低，提高了齿廓的啮合性能，能够满足高精度场合下的使用要求。

　　0 引言

　　谐波减速器具有减速比大、结构简单、精度高等优点，因此被广泛应用于机器人、航空航天和军事等对于精度要求较高的领域。目前在啮合理论方面，主流的方法有基于Willis定理的包络法、改进运动学法和瞬心线法。在谐波传动齿廓方面主要出现过直线齿廓、渐开线齿廓、圆弧齿廓及S型齿廓。直线齿廓是谐波传动的发明者Musser提出的，但该齿形没有考虑柔轮的变形所引起的位移与转角误差。渐开线齿廓的研究已趋于成熟，但在谐波运动的啮合过程中由于共轭啮合区域较小，且会产生尖点啮合情况，这些会造成接触点应力的急剧增大，大幅缩短齿廓寿命。圆弧齿廓是目前国内研究最多的齿廓齿形，与渐开线齿廓相比，其具有啮合齿数多的优点， 改善了应力状况与啮合质量，但双圆弧齿廓的侧隙不均匀，部分区域存在侧隙较大的情况。S型齿廓由日本学者Ishikawa等在1989年基于齿条近似法提出，根据映射关系可以实现与同类齿廓的连续接触。但这类齿廓大多都是在无穷齿数下的近似设计，并未考虑实际运动过程中的转角影响。基于此，本文综合考虑了谐波传动的弹性变形、齿轮偏转角、波发生器类型等因素，根据运动件的几何关系和啮合矩阵，通过曲线映射的方式得到原始凸齿廓，根据改进法对原始齿廓进行修形，接着根据修形完成的凸齿廓求解两段凹齿廓，并最终与传统S型齿廓进行对比。

　　1 S型齿的齿廓设计

　　柔轮与刚轮间转角关系：固定波发生器坐标系，并以波发生器的回转中心o为原点，长轴为y轴，建立坐标系，则波发生器、柔轮、刚轮之间的运动关系如图1所示。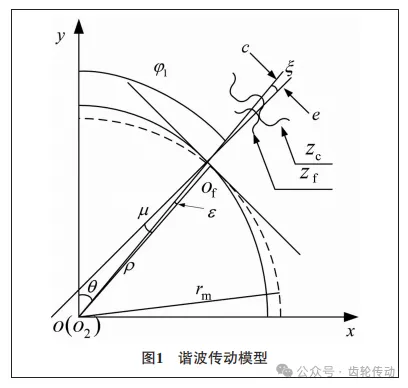

      为了方便计算，本文的波发生器将采用余弦曲线，根据柔轮中性层的不变形理论，可以将其看作波发生器的等距曲线，则柔轮中性层曲线在极坐标下可以表示为

      式中：k为径向变形系数，m为模数，rm为柔轮的中性层半径。

　　rm大小可以通过柔轮分度圆半径求解：

      波发生器装配后迫使柔轮发生变形，其中柔轮轮齿的法向转角可以表示为

      根据中性层不伸长理论，其柔轮变形后转过的弧长应与未变形前扫过的弧长保持一致，因此有

      为了便于计算，因此整理时忽略其高阶项，通过计算其一阶近似积分可以得到

      根据理论传动比可以得到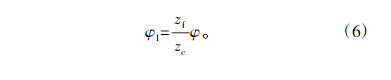

      其余的转角关系可以通过图1中的几何关系可得：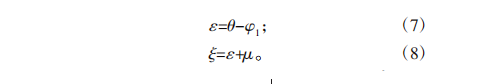

　　表1 谐波传动各角度参数含义

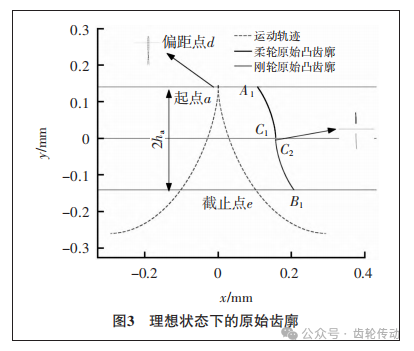
　　传动齿廓设计：根据齿条近似法原理，当刚轮的齿数无穷大时，此时柔轮将相对于刚轮沿着运动轨迹平移。图2为齿条近似原理图，其中AB曲线为柔轮相对于刚轮的运动轨迹，将A点作为映射的起始点，将B点作为映射的结束点，按照0.5倍的比例进行曲线映射，得到了刚轮凸齿廓BC与柔轮凸齿廓AC，由于曲线映射的关系，柔轮与刚轮齿廓均保留了运动轨迹的特征，即柔轮凸齿廓与刚轮凸齿廓间将实现连续啮合。其中柔轮中性层在刚轮坐标下的运动轨迹AB 的轨迹方程表示为：

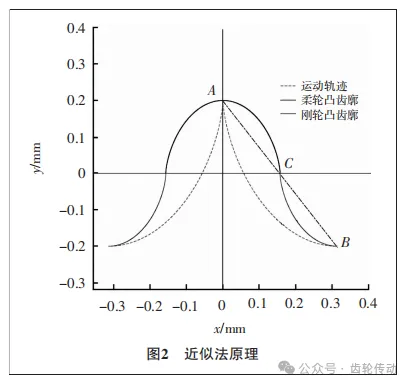
　　由于原始曲线在(-π/2，π/2)内的运动轨迹存在偏距点，考虑到齿廓间连接的顺滑性，因此设计段内不能包含凹凸性突变的情况，因此映射的起始角度ηd应取运动轨迹二阶导数为0时对应的点，假设偏距点为d，则e为曲线映射的截止点，其角度可以表达为ηe=arccos(1-2h*a /k)，其中h*a为齿顶高系数。因此原始刚轮凸齿廓表达式为：

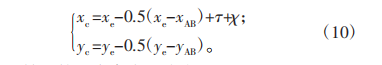
　　原始柔轮凸齿廓表达式为：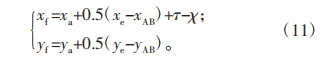

　　2 齿廓修形

　　传统齿廓修形：在求解原始齿廓时，做了柔轮与刚轮的齿数均是无限的假设，然而在实际运动过程中，柔轮齿廓除了沿着运动轨迹平移外还存在齿廓本身的旋转角度，因此需要对原始齿廓进行修形。根据坐标系之间的转化原则，一开始的原始曲线M是建立在中性层上面的，而柔轮的齿顶相对于刚轮的运动轨迹则需要建立在柔轮的分度圆上，因此运动轨迹M0需要在原始曲线M的基础上向上平移一段h。h可以表示为

　　传统的修形方法是假设理想啮合条件下柔轮齿廓与刚轮齿廓的啮合点为P，但由于转角影响的存在，柔轮在啮合点P处沿着N旋转了ζ，从而柔轮与刚轮齿廓将产生干涉，干涉量可以通过啮合点P的位移PB来表示。如图4所示，F点为柔轮原始齿廓法线与中心线的交点，由于旋转角度ξ较小，因此点P在转角ξ的影响下产生的位移PB可以用弧长FA代替，其表达式为

　　式中，lNF为线段NF的长度。

　　lNF的表达式为

　　式中：(xP，yp )为P点坐标，(xN，yN )为N点坐标，α为接触点压力角。

　　α的计算公式为

      因为ξ较小，于是将上述弧长FA近似看作齿廓x方向上的修型量，将其定义为Δx，将变形量平均分配给刚轮与柔轮，原始曲线的映射初始角为ηd，映射结束角度为ηe，因此柔轮齿顶轮廓的表达式为：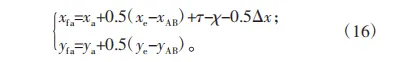

      刚轮的齿顶轮廓表达为：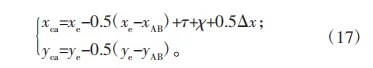

      根据齿条近似法，柔轮与刚轮的凹齿廓同样可以通过凸齿廓的映射所得到，但为了保证柔轮与刚轮齿廓啮合的过程中不产生干涉，要在映射的齿廓上加入间隙调整量，于是柔轮的凸齿廓表达式为：

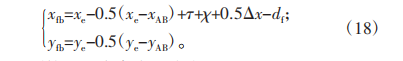
　　刚轮的凸齿廓表达式为：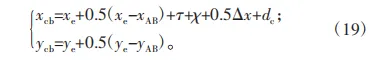

　　由于映射起始点并不为0，因此凹齿廓与凸齿廓间存在空白区域，需要通过过渡直线连接，通过刚轮与柔轮两端齿廓的端点，可以得到过渡直线段表达式：

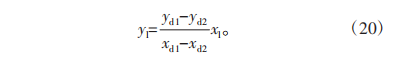
　　式中，(xd1，yd1)和(xd2，yd2)为凸齿廓与凹齿廓表达式的端点。

　　传统的S型齿廓修形方法啮合区域较小，且侧隙在啮和区间内变化较大，难以满足对精度要高的场合，因此本文提供了一种新的修形方式来解决这些问题。

　　改进法齿廓修形：根据齿轮啮合原理中的坐标系变换原理，柔轮固定坐标系可通过坐标系变化矩阵Mcf和底矢变化矩阵Wcf变化到刚轮坐标系，其中矩阵Mcf和矩阵Wcf表示为：

　　而刚轮坐标系转换到柔轮坐标系的坐标变换矩阵Mfc和底矢变换矩阵Wfc分别表示为：

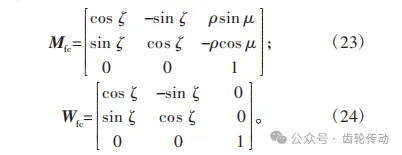
　　根据上述表达的矩阵，我们可以得到柔轮齿廓坐标在刚轮固定坐标系下的坐标表达式为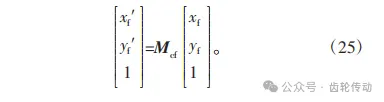

      同样的刚轮齿廓坐标点在柔轮坐标系中的坐标表达式为

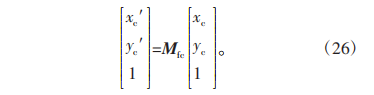
　　为了分析原始柔轮凸齿廓相对于刚轮的运动状态，直观地反映装配后谐波传动齿廓的啮合情况，在将柔轮凸齿廓与刚轮凸齿廓分别转换到各自坐标系后使用啮合矩阵Mcf，得到了图5所示的(0，π)区间内柔轮的运动轨迹图。

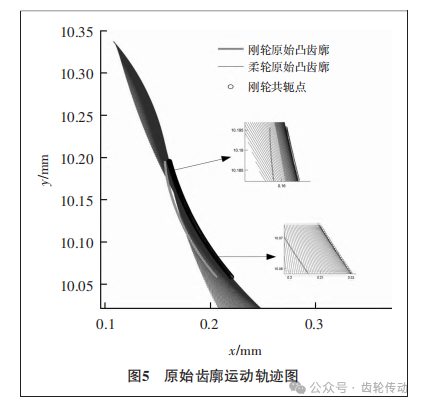
　　通过boundary函数查找柔轮运动轨迹的边缘轮廓，通过处理可以得到刚轮的共轭点。将刚轮的共轭齿廓与刚轮的原始齿廓间的差值作为修形量进行第一次修形。假设刚轮的共轭曲线的横坐标为xca1，则修形量可以表示为

　　那么第一次修形后柔轮齿顶轮廓的表达式为：

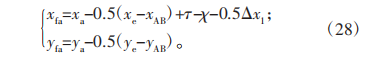
　　刚轮的齿顶轮廓表达式为：

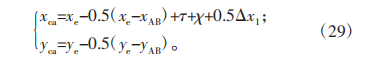
　　将第一次修形后的柔轮齿廓与刚轮齿廓再次代入啮合矩阵Mcf中，并再次查看啮合情况。

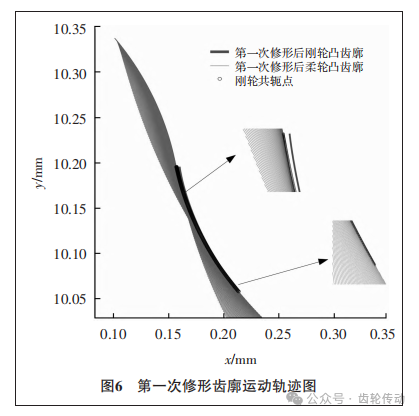
　　我们发现经过第一次修形后刚轮凸齿廓末端啮合情况较好，而初始端的侧隙较大。这是因为修形时齿廓末端所采用的共轭点是由柔轮凸齿廓末端所构成的，因此将此处的修形量均分给2段原始齿廓是合理的。然而初始端的共轭点并非由柔轮原始凸齿廓的初始端所构成，因此在此处将其作为修形量不合理。针对这种情况，采取对齿廓进行二次修形的方式来降低初始段的侧隙。同样使用boundary函数提取出刚轮的共轭点，假设此时刚轮的共轭曲线的横坐标为xca2 ，则修形量表示为

　　那么经过二次修形后柔轮的齿顶轮廓表达式为：

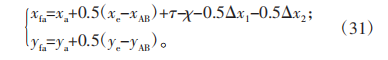
　　刚轮的齿顶轮廓表达为：

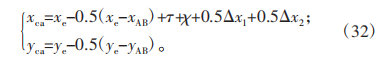
　　将二次修形后的柔轮齿廓代入啮合矩阵Mcf，查看刚轮初始段的侧隙情况。

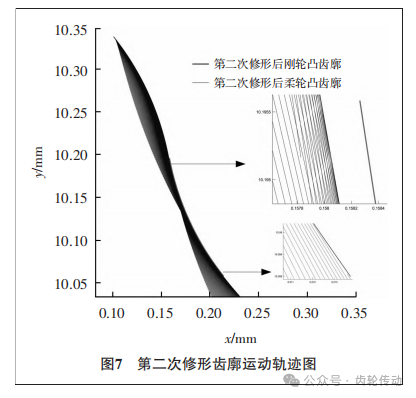
　　通过图7可以看到刚轮初始端依然存在过度修形的情况，但此时上端的侧隙分布已经处于0.5μm以下，属于合理范围之内，故不再对凸齿廓进行第三次修形。至此，柔轮与刚轮的凸齿廓修形完毕。根据修形后的刚轮凸齿廓，通过使用啮合矩阵 Mfc，采用刚轮包络柔轮的方法，计算出刚轮的运动轨迹。同样采用boundary函数提取柔轮的共轭点，通过这种方式，可以得到与刚轮凸齿廓共轭的柔轮凹齿廓。

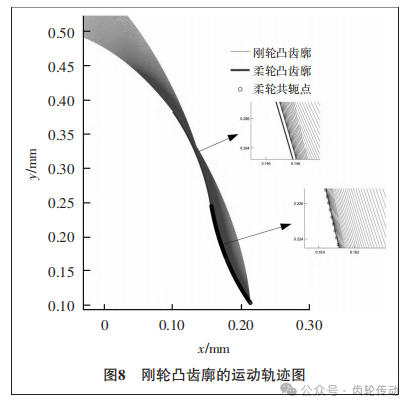
　　用上述的方法同样可以求解刚轮凹齿廓，基于柔轮的运动轨迹，通过柔轮凸齿廓求解刚轮的共轭凹齿廓。

　　表2 齿形设计与修形相关参数

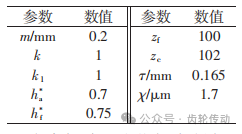
　　表2为本文齿廓设计的参数，下面将对本文提到的两种平面设计的齿廓进行啮合性能分析，主要从传动侧隙、共轭区域及瞬时传动比展开分析。

　　3 齿廓分析

　　侧隙分析：柔轮的啮合状态的好坏可以大致通过齿廓侧隙这个指标来判断。从侧隙的大小与分布可以初步判断传动过程中稳定性，齿间载荷分布于是否产生干涉。首先建立侧隙计算模型。通过将齿廓曲线离散成点，求解当波发生器旋转过一定角度下时，每个柔轮齿廓与刚轮齿廓间的最小距离即为侧隙lfc。

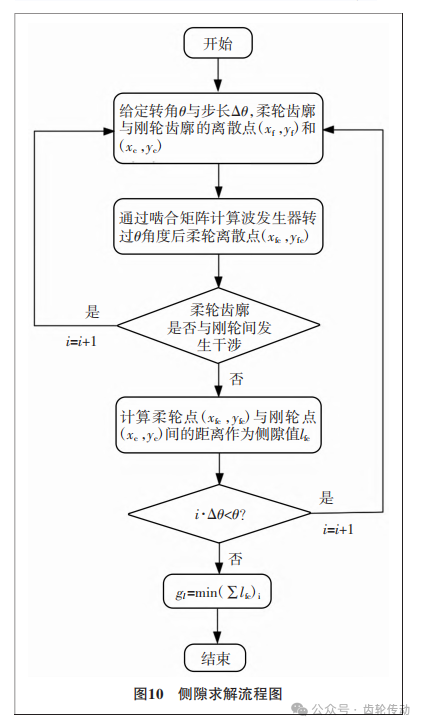
　　通过图11的左侧可以看到凸齿廓与凹齿廓间存在空白区域，这是由于初始映射角非零导致的，因此在最终的齿廓中使用直线过渡段将两段齿廓连接。因为刚轮与柔轮的凹齿廓是在凸齿廓的基础上施加间隙调整量后得到的，因此刚轮与柔轮齿廓在完全啮合状态下间隙均匀稳定。

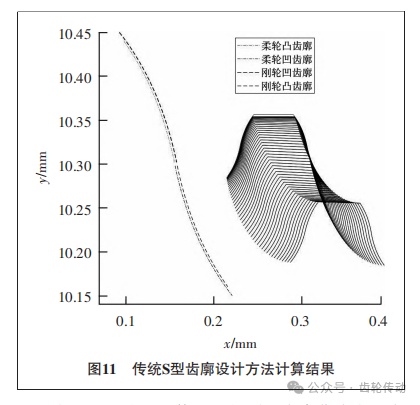
　　由于通过改进法修形后得到的齿廓曲线在凸齿廓顶端存在一定的过度修形，因此在完全啮合状态下两齿廓的间隙呈现出中间大、两边小的趋势。由于改进法的凹齿廓是根据共轭点求得的，因此没有明显的连接空白区域。

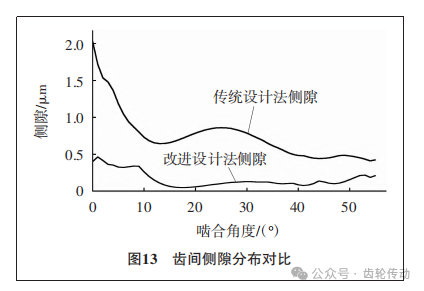
　　从图13可以看出，与传统法相比，改进法设计下的齿廓侧隙整体更小，且更加平稳。传统S型齿廓设计方法由于凹齿廓是直接由凸齿廓映射所得，因此在啮合区整体侧隙偏大，而在啮入区的侧隙则有所下降。由于改进法设计下的S型齿廓在凸齿廓初始端存在一定的过度修形，因此在啮合区的侧隙相对于啮入区有所上升，但上升的幅度较小，整体侧隙分布情况趋于稳定，在一定程度上提高了回转精度。

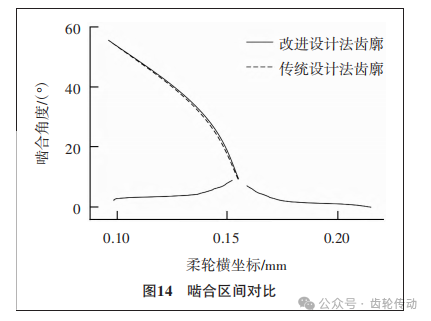
　　啮合区域分析：柔轮齿廓与刚轮齿廓的啮合大致可以分为2个区域：1)啮合区。此时柔轮凸齿廓与刚轮凹齿廓间会产生啮合，与此同时柔轮凹齿廓与刚轮凸齿廓同样将发生接触。2)啮入区。柔轮凸齿廓与刚轮凸齿廓间在这个区间内将产生啮合，此区域也是谐波传动的主要啮合区。因此计算啮合区间时需要进行分段求解。 两种修形方法计算出的啮合区间如图14所示。 由于传统修形法的凹齿廓采用直接映射的方式，因此凸齿廓与凹齿廓在啮合的过程中不发生接触，因此在整个运动过程中只有两段凸齿廓发生共轭，因此该设计方法下只有一段啮合区间。而改进法下的凹齿廓是根据运动轨迹包络求得的，因此即使是在啮合区内也有较好的接触情况。两种修形方法均在[9.334°，55.645°]的区间内发生共轭，而通过改进法设计的柔轮齿廓，在[2.154°，7.18°]区间实现了两点共轭，与此同时柔轮的凸齿廓在[2.154°，8.975°]和 [9.334°，55.645°]区间上分别实现了与刚轮凹齿廓与凸齿廓间的啮合，实现了二次共轭，证明了改进法设计的齿廓增大了共轭区域，降低了柔轮啮合过程中的轴向应力，提高了传动效率，使得传动更加可靠，在一定程度上延长了减速器的使用寿命。

　　瞬时传动比：通过平均积分角速度求得的传动比只能从宏观角度上描述谐波减速器的运动状况，但实际上谐波减速器的瞬时传动比是变化的。瞬时传动比的波动会直接影响减速器运行的稳定性，而传动比误差既来源于中性层曲线的形状也取决于齿廓曲线。如图15所示，当波发生器固定时，若柔轮非变形端以恒定角速度ω1回转，则在变形端上的点c将以瞬时角速度ω1c围绕中性层曲线在c点处的曲率中心os 回转，由于线速度相等，故有

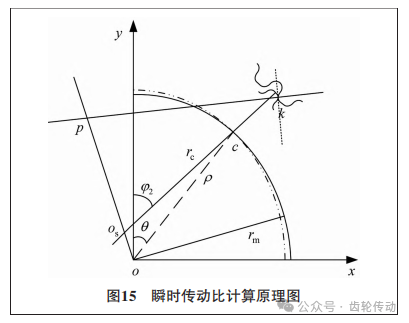
　　若刚轮的角速度设为ω2，此时的瞬时传动比将表示为

　　其中，i为理论传动比，其大小为

　　根据Willis定理，若两齿廓的接触点为k，则经过k点的公法线与瞬时回转中心连接线oos的交点p就是瞬时啮合节点。故啮合节点的瞬时传动比可以表示为

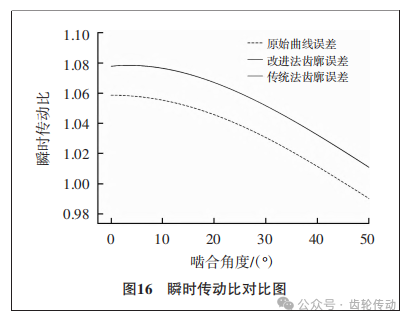
　　因为两种修形方法均采用相同的中性层曲线，故原始曲线误差相同。通过式(34)和式(36)可以发现瞬时传动比的波动幅度在一定程度上与瞬时曲率中心直接关联，通过计算发现中性层半径越大，径向变形量越小，瞬时传动比就越趋于稳定。

　　由于谐波减速器多齿啮合的特性，其传动误差将会被均化，因此对求解得到的瞬时传动比曲线积分后进行叠加。计算后发现改进法设计下的齿廓传动误差为3.96%，而传统修S型齿廓误差为3.962%。相对于传统S型齿廓，改进法设计下的齿廓传动误差略有降低，性能提升了约0.05%，这也意味着齿廓曲线对于瞬时传动比的影响较小。同时在误差曲线积分时发现，啮合齿数也是影响传动误差的关键因素。随着啮合齿数的增加，原始曲线的误差将逐渐趋向于0，此时传动误差将主要体现为齿廓曲线误差，整体的传动误差将得到明显的降低。

　　4 结论

　　本文提出了一种区别于传统S型齿廓设计的方法。与传统S型齿廓相比，改进法设计的S型齿廓具有侧隙更小、共轭区间更大、传动误差更小的特点，可以满足高精度场合下的使用要求。由于柔轮的轨迹曲线存在偏距，为了保证齿廓曲线连接的顺滑性，齿廓的映射设区域应不包含曲线上凹凸性突变的点，即映射起点应为运动轨迹二阶导数为0的点，且为了保证原始齿廓有足够的映射区域与齿廓间的平滑连接，变形系数k的取值范围应在[0.9，1.1]内。齿廓的类型对瞬时传动比的影响较小，而中性层曲线的类型，中性层半径与径向变形量对瞬时传动比的影响较大，在设计时应优先考虑大半径、小变形量的设计方案。

　　作业来说，精度较高，所以该控制器可实现良好的轨迹跟踪控制。

　　4 结语

　　本文针对飞机牵引系统的自动控制问题进行研究，设计了基于Fareh控制策略的非线性控制器，通过控制牵引点的速度大小与方向来实现飞机的轨迹跟踪与姿态调节。通过MATLAB/Simscape对系统进行仿真模拟，验证了所设计控制器的可行性。

　　参考文献：略。