时间:2024-09-18来源:北京精密 作者:江山
[编者按] 谐波齿轮传动具有传动速比大、精度高、回差小、体积小和重量轻等优点,广泛应用于工业机器人等诸多精密传动领域。天津工业大学陈晓霞教授团队在谐波齿轮传动的啮合理论、柔轮空间变形、共轭齿廓设计、啮合状态可视化及有限元仿真分析、基于齿廓测量数据的传动状态仿真及传动误差分析等方面,开展深入研究。提出共轭区间存在性和共轭齿廓可用性判定方法,获得三圆弧齿廓、公切线双圆弧齿廓和摆线齿廓谐波齿轮发明专利;建立基于强制几何约束条件和基于力平衡连续性条件的柔轮计算模型,完善了中面不伸长理论;提出基于等分弧长等算法的谐波齿轮装配模型数字化样机,实现了谐波齿轮啮合状态的可视化;建立基于齿廓测量数据的谐波齿轮有限元模型,得到能反映加工偏差的轮齿啮合状态仿真,使负载啮合状态和传动误差的仿真分析成为可能。本公众号分3期,介绍陈教授团队的创新成果。

陈晓霞简介:工学博士,天津工业大学教授,博士生导师。从事高等教育30多年,主要研究方向为谐波齿轮传动、数字化设计、基于装配的建模仿真。获天津市高校学科领军人才、天津工业大学优秀教师和天津市工程专业学位硕士研究生优秀学位论文指导教师称号。主持完成国家自然基金面上项目、天津自然科学基金重点项目和面上项目、教育部科学技术研究重点项目各1项;参与完成天津市自然科学基金重点项目和天津市教委项目各1项,主持完成浙江大学CAD&CG国家重点实验室开放课题2项;参与完成各类项目10余项。发表论文70余篇,被SCI/EI收录30余篇。主编专业书籍2部、参编5部。主要亮点:
1. 基于强制几何约束条件和基于力平衡连续性条件,提出考虑中性层伸缩变形的柔轮计算模型,定量地给出了更接近工程实际的柔轮齿圈中面伸长的计算方法。提出了基于变形后柔轮齿廓位置的等分弧长定位方法,为准确定位轮齿提供了更合理的计算方法,使谐波齿轮装配模型数字化样机更接近实际,开发基于柔轮三维变形特征的谐波齿轮数字化样机,实现啮合齿对间微米量级侧隙的仿真分析和可视化。对正确呈现谐波齿轮传动状态、实现谐波齿轮的高效设计与优化,提供评价手段。
2. 改进了谐波齿轮传动齿廓设计方法中的两项近似计算,实现更准确的柔轮齿面定位,提升了共轭齿廓设计方法的严谨性。提出共轭方程解存在性的图形表达方法,据此判定共轭方程解存在性及共轭齿廓可用性,揭示柔轮空间变形规律及原始齿廓参数对齿廓共轭方程解存在性的影响,明确了各参数对共轭方程解的存在条件及存在区间的影响规律,定量评价原始齿廓,指导共轭齿廓求解。
3. 提出基于柔轮空间变形特征的谐波齿轮空间齿廓设计、齿廓拟合和侧隙评价验证新方法,为精密谐波齿轮传动的啮合分析和齿廓设计提供理论依据;基于啮合点周向刚度和齿间侧隙分布迭代计算啮合力,获得基于接触分析的多齿啮合力分布规律,为基于侧隙和啮合力合理分布的圆弧齿廓优化设计提供了可行途径。提出基于线接触的三圆弧空间齿廓设计方法,沿齿长方向形成线接触啮合,从而增大啮合接触面,降低传动应力。据此申报公切线双圆弧齿廓、三圆弧齿廓、摆线齿廓的谐波齿轮传动发明专利。
4. 建立了更为精确反映齿廓和柔性轴承的实体单元有限元模型,更真实地反映柔轮在空载和负载工况下的实际变形。提出了基于有限元模型的齿廓侧隙计算方法,用以评估空载啮合特性。在空载装配模型上施加不同工况的负载扭矩,能够定量评价谐波齿轮在负载条件下的多齿啮合状态和整机传动性能,为齿廓方案改进和结构优化设计提供有效手段。对于设计方案的改进,提高谐波齿轮的承载能力和耐用性具有重要意义。
5. 提出基于齿廓测量数据的谐波齿轮传动性能的理论分析和有限元仿真方法,更准确呈现谐波齿轮啮合状态和传动性能。为谐波齿轮的性能评价提供新方法,弥补物理样机只能测试整体性能而无法测定细节状态的不足。
谐波齿轮传动
创新研究1:波发生器作用下的柔轮变形计算与分析1.1 基于薄壁圆环模型的变形理论
谐波齿轮减速器是基于柔轮弹性变形的齿轮传动机构,柔轮的变形对齿廓设计和啮合质量有至关重要的影响。圆环模型(图1a、1b)是柔轮变形分析和计算的基础理论模型。课题组研究了圆环模型变形的强制几何约束、力平衡及连续性等条件,对包括四滚轮、双圆盘和凸轮(图1c)等多种波发生器作用形式下柔轮变形分析的圆环模型进行了受力分析,研究了考虑力学作用(图1d)的柔轮中性层变形(图1e)。提出了凸轮作用形式下基于包角分段的内力和变形计算方法,能够在具有配合间隙的条件下准确计算变形内力和位移(图1f)。
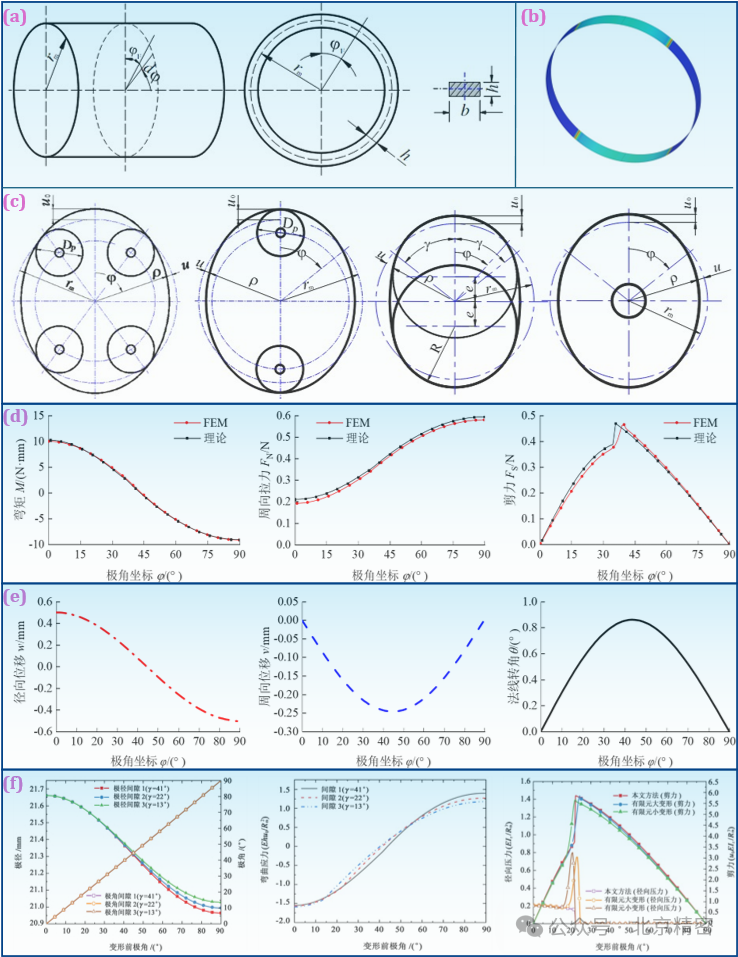
图1 波发生器作用下柔轮变形的圆环模型及其受力变形:(a) 圆环模型; (b) 圆环变形有限元模型; (c) 常见的波发生器作用形式; (d) 圆环变形时的受力结果; (e) 圆环变形的位移结果; (f) 具有配合间隙时的圆环变形结果.
1.2 柔轮的三维空间变形计算与分析(1) 齿圈变形常见的杯形和礼帽形柔轮在其隔板结构的约束下,产生的变形并非圆环模型假设的二维平面问题,而是一个具有轴向翘曲的复杂空间变形问题。基于圆柱筒变形的直母线假定,课题组基于柔轮空间变形模型(图2a)研究了齿圈端前、中、后截面上的变形运动轨迹(图2b)和变形位移(图2c),并沿轴向对直母线假定进行了准确性验证。图2d和e分别为长轴和短轴处沿轴向的径向位移结果,图2f为柔轮45°位置处变形后的周向位移结果。结果表明杯形和礼帽形柔轮变形后其母线近似呈线性的精度较高,但直母线假定忽略了柔轮的轴向位移,导致理论截距和斜率具有一定的偏差(图2d-f)。
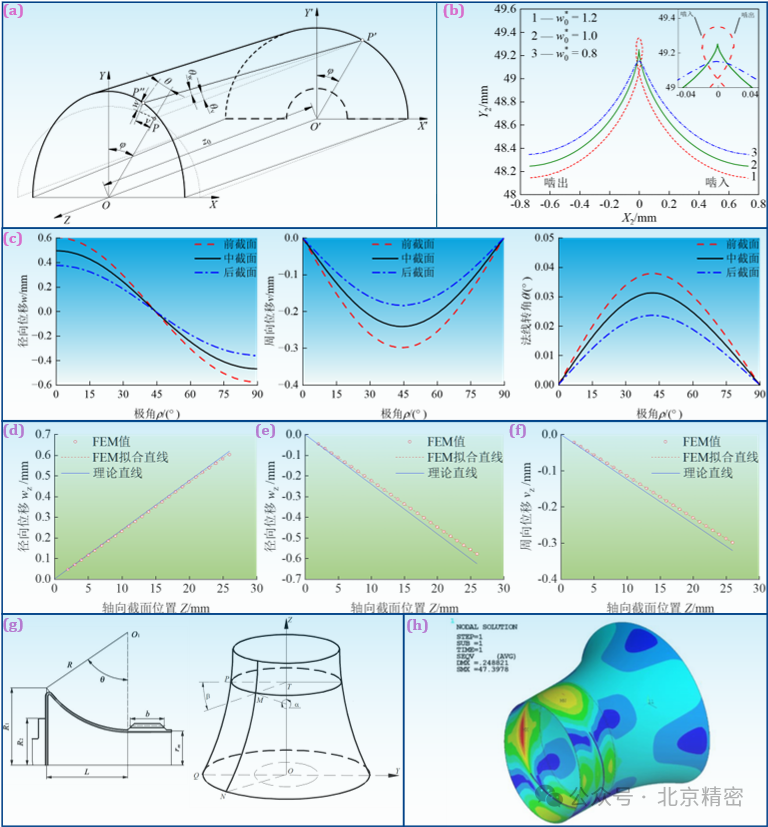
图2 柔轮的三维空间变形特性:(a) 柔轮空间变形示意图; (b) 齿圈不同截面上变形运动的三种特征轨迹; (c) 齿圈前中后三截面上的位移结果; (d) 柔轮长轴上沿轴向分布的径向位移结果; (e) 柔轮短轴上沿轴向分布的径向位移结果; (f) 柔轮45°位置处沿轴向分布的周向位移结果; (g) 钟形柔轮结构示意图; (h) 钟形柔轮有限元模型的变形.
如图2a中所示的柔轮空间变形中,齿圈部位从前端到后端渐变的变形特征使得齿形的设计变得极其复杂。钟形柔轮(图2g-h)中筒壁母线不为直线,在变形时能够吸收变形,最终使得齿圈部分变形后呈椭圆柱状,不具有显著的锥度特征,可以二维截面变形来简单描述。这将降低齿形设计的复杂性。为了探究钟形柔轮齿圈变形的机理,课题组对腹板内收和外翻两种结构进行了力学分析,推导出实现齿圈平面变形时的连接条件。(2) 齿圈的中性层轮齿使得齿圈的实际中性层相对几何中性层存在偏移(图3a),且由于轮齿的不连续性实际中性层不再是圆柱面。这就导致在中性层上确定轮齿变形后位置的计算出现偏差,无法对齿圈变形和轮齿定位进行有效计算。课题组在齿圈上定义了一个圆柱面:该圆柱面沿周向应变虽然不恒为零,但在一个齿距内的应变积分等于零(即一个齿距内弧长不变),即齿圈的等效中性层。在此基础上计算了等效中性层与简单几何中间层之间的偏移率(图3b),并研究了其对齿高、齿厚和齿根圆角半径的敏感性(图3c),最后对敏感参数进行量纲分析与仿真实验,根据量纲分析的结果(图3d)根据给出了偏移率计算经验公式。

图3 轮齿影响下的齿圈中性层:(a) 齿圈中性层示意图; (b) 中性层偏移率计算方法流程图; (c) 偏移率的敏感性分析结果; (d) 偏移率的量纲分析结果.(3) 隔板变形与应力
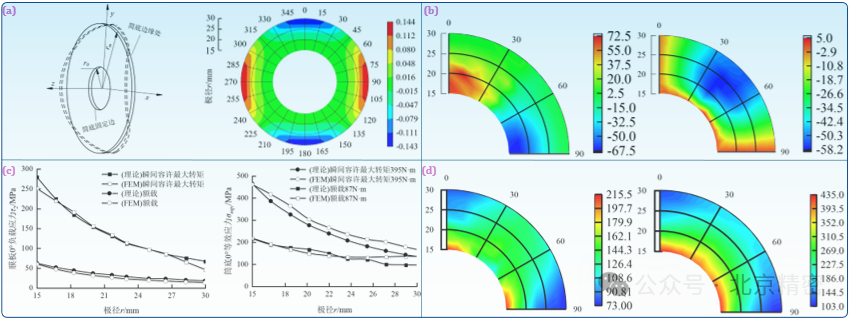
图4 柔轮筒底隔板圆盘的变形和应力:(a) 隔板变形的示意图及理论变形结果; (b) 装配变形下隔板应力的理论结果; (c) 装配与负载状态下隔板应力的变化规律; (d) 负载工况下隔板应力的理论结果.
结构扁平化是谐波减齿轮的主要发展方向之一,但随着柔轮轴向尺寸的相对减少,此前在长筒条件下对轴向位移忽略不计的假定将带来越来越大的偏差。图2中已展示了在隔板约束下柔轮将产生空间的锥度状变形,当柔轮长径比降至1/3时,筒底的变形及其应力也产生了显著的影响。为揭示超短筒谐波齿轮柔轮筒底装配变形及应力形成机理,课题组建立了样条函数表达的筒底隔板圆盘弯曲变形模型(图4a),提出了隔板的挠度变形和应力的理论计算方法,分别计算了装配和负担扭矩状态下的隔板应力(图b-d)。(4) 波发生器
除了波发生器迫使柔轮发生变形之外,柔性轴承在凸轮作用下的变形也是值得关注的研究内容。在滚珠的往复接触和摩擦下,柔性轴承的故障也是谐波齿轮减速器失效的主要原因之一。因此,分析柔性轴承的实际工作状态,判断滚珠的实际接触位置和接触里分布特征具有现实的工程意义。课题组基于集中力作用下的圆环变形模型(图5a),提出滚珠多角度接触力叠加法迭代计算模型,实现了柔性轴承滚珠实际接触的理论判断和接触力的计算。建立了柔性轴承与柔轮间接触的有限元仿真模型(图5b),充分考虑了轴承内外环与滚珠间的接触关系,验证了滚珠的接触,分析了滚珠与沟道之间的接触应力(图5c)。

图5 柔性轴承变形的滚珠受力与接触分析:(a) 集中力作用下的圆环变形计算; (b) 柔轮轴承与柔轮间接触的有限元分析; (c) 柔性轴承的有限元接触模型及滚珠的接触应力; (d) 滚珠接触状态的有限元分析.
标签: 谐波齿轮传动
免责声明:凡注明(来源:齿轮头条网)的所有文字、图片、音视和视频文件,版权均为齿轮头条网(www.geartoutiao.com)独家所有,如需转载请与本网联系。任何机构或个人转载使用时须注明来源“齿轮头条网”,违反者本网将追究其法律责任。本网转载并注明其他来源的稿件,均来自互联网或业内投稿人士,版权属于原版权人。转载请保留稿件来源及作者,禁止擅自篡改,违者自负版权法律责任。
相关资讯