摘要 基于空间展成法加工原理，推导了等变位斜齿锥齿轮的齿面数学模型和齿面接触线方程，建立了7 齿对齿面接触的有限元动态分析模型，获得了啮合周期内边缘接触的位置、不同负载下齿面接触应力和齿根弯曲应力的变化曲线，分析了斜齿锥齿轮稳定啮合时法向接触力的变化规律和轮对重合度。结果表明，斜齿锥齿轮齿对在进入和退出啮合时均发生了边缘接触，整个啮合过程的接触力曲线较为平滑，在3 齿啮合区附近呈近对称分布且具有较高的重合度，最大弯曲应力出现在大轮大端和小轮小端的齿根过渡圆角附近。

　　关键词 斜齿锥齿轮 等变位 边缘接触 接触力 有限元分析

　　0 引言

　　斜齿锥齿轮相较直齿锥齿轮具有高重合度系数、高承载能力、传动平稳等特点，是高速重载传动系统中十分重要的零部件[1]652。学者们已利用球面渐开线齿廓生成原理及共轭啮合原理实现了斜齿锥齿轮的参数化设计和虚拟加工[1]653-655[2]246-249[3]，由于斜齿锥齿轮齿面的独特性和复杂性，需要对其在实际工程中的啮合特性进行深入研究，特别是对于实际加载啮合中的受力和边缘接触情况，应结合其齿面数学模型进行有限元分析，为斜齿锥齿轮传动的设计和应用提供依据。

　　学者们对锥齿轮啮合特性开展了大量研究分析。王中荣等[4-5]利用有限元法研究了直齿锥齿轮轮齿的接触应力分布、变形规律和齿根弯曲应力。Litvin等[6]利用有限元法研究了弧齿锥齿轮加载啮合时的最大接触应力和最大齿根弯曲应力，并且找到其边缘接触区域。邓拥军等[7]运用有限元法研究了弧齿锥齿轮在不同载荷和安装误差下的接触斑点及接触轨迹的变化规律。侯祥颖等[8]69-73利用有限元软件进行了考虑边缘接触的弧齿锥齿轮加载接触分析，定量分析了边缘接触轨迹随载荷增加的变化规律。但是，国内外缺少等变位斜齿锥齿轮加载接触分析方面的研究文献，斜齿锥齿轮啮合过程中接触力的分析比较少见。

　　本文中基于空间展成法加工原理，建立了等变位斜齿锥齿轮副的齿面方程及其有限元模型，分析了变载荷条件下斜齿锥齿轮齿对啮合周期内的齿面接触应力和齿根弯曲应力以及齿轮接触力的变化规律和轮对重合度。

　　1 数学模型

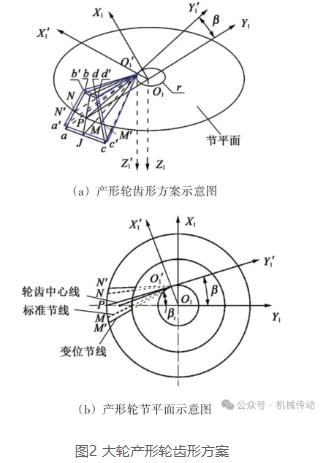
　　本文中在已有研究的基础上，通过空间展成法推导出等变位斜齿锥齿轮的齿面方程[2]246-248。如图1所示，产形轮与被加工齿轮以传动比i啮合传动，产形轮齿面包络生成被加工齿轮齿面，与产形轮固联的坐标系为S₁，与被加工齿轮固联的坐标系为S_P，Σ 为两齿轮中心轴线Z1和ZP 的夹角。

　　大轮产形轮的齿形方案如图2 所示。O1'ab、O1'cd 均为切向变位前的齿面;O1'a'b'、O1'c'd' 均为切向变位后的齿面;齿面倾斜角为压力角α ;点P 为齿面上节线O1'N、O1'M 端点间圆弧中点;O1'P 为轮齿中心线;平面O1'JP 垂直于节平面且与图中半径为r 的圆相切于点O1' ;β 为齿倾斜角;节平面上的齿厚弧长PN=PM=S ∕ 2=πm ∕ 4;O1'N'、O1'M' 均为变位节线;切向变位弧长NN'=MM'=xt ·m ;S 为节圆齿厚;m 为齿轮模数;xt 为切向变位系数。大轮产形轮采用切向正变位对应齿面方程中的xt 为正值，而小轮产形轮采用切向负变位对应齿面方程中的xt 为负值，且两者互为相反数;大轮与小轮轮齿中心线O1'P 关于O1Y1 轴对称，其他参数相同。

　　在固联坐标系S₁ 中，产形轮齿面的参数方程和法矢量方程为

　　式中，u₁ 、θ₁ 均为产形轮齿面的参数;M 为齐次坐标变换矩阵;矩阵L 由M 去掉第4行和第4列得到。

　　对于大轮产形轮，式(1)中矩阵M 表达式为

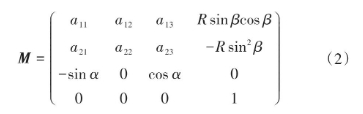
　　式中，矩阵各分量分别为

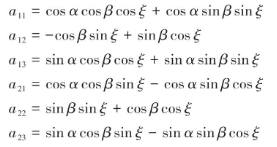
　　式中，ξ 为图2(b)中节平面上轮齿中心线O1'P 与变位节线O1'N' 的夹角，表达式为

　　式中，矩阵各分量分别为

　　上述式中，z 为产形轮齿数;x_t 为切向变位系数。

　　被加工齿轮齿面与产形轮齿面互为共轭齿面，则在与被加工齿轮固联的坐标系SP 中，被加工齿轮的齿面方程和法矢量方程分别为

　　式中，M_P1 为坐标系S₁ 到坐标系S_P 的变换矩阵;矩阵M_P1中的Σ 为两齿轮的轴交角;φ₁、φ₂ 分别为产形轮齿面和被加工齿轮齿面到达啮合位置所转动的角度;矩阵L_P1 由M_P1 去掉第4 行和第4 列得到。M_P1 的表达式为

　　式中，矩阵各分量为

　　根据齿轮接触条件[9]，得大轮和小轮啮合时的齿面接触方程为

　　式中，r₁ 、r₂ 分别为小轮和大轮在同一坐标系中的齿面方程;n₁ 、n₂ 分别为小轮和大轮在同一坐标系中的齿面法矢量方程。

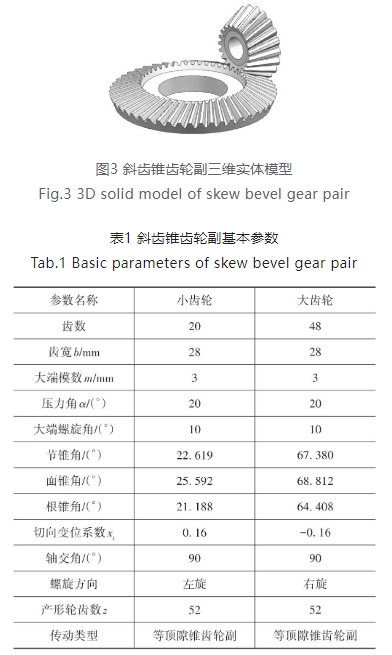
　　根据上述被加工齿轮齿面的数学模型，考虑表1中所示斜齿锥齿轮副的基本参数，根据式(1)～式(4)求解齿面离散点坐标，使用NX 软件对被加工齿轮齿面进行重构，建立等变位展成斜齿锥齿轮副三维实体模型，如图3所示。

　　2 有限元模型

　　将斜齿锥齿轮的三维几何模型导入Hypermesh中进行结构化网格划分。将齿轮切割得到单个轮齿，再对单个轮齿剖分为6 部分，进行结构化网格划分。根据齿面接触斑点连续的网格尺寸条件[10]，分别在工作齿面齿高方向划分40 层单元，在齿根过渡部分划分10 层单元，在齿宽方向划分140 层单元。综合考虑模型计算精度和计算时间，分别对大轮与齿轮中心轴线上的参考点建立受力耦合约束，对小轮与齿轮中心轴线上的参考点建立运动耦合约束，划分的单齿啮合有限元网格模型如图4所示。

　　为保证齿面接触分析的稳定性和收敛性，在Abaqus 动态分析环境将分析过程分为3 步：①小轮绕齿轮轴线施加微小转动量，使小轮与大轮齿面接触;②利用幅值曲线中的平滑分析步，使绕大轮轴线的负载转矩缓慢增大到给定值;③给小轮施加绕轴线转动一定角度，使小轮驱动大轮转动。

　　齿面接触分析时，在齿面接触斑点连续的同时，也需要考虑接触单元的数量对计算结果精度的影响。本文中选取斜齿锥齿轮单齿啮合有限元模型验证所划分单元的有效性。小轮完整啮合周期的瞬时接触线如图5 所示，根据齿面接触方程式(6)可以得到斜齿锥齿轮副瞬时接触线为空间直线[11]。小轮完整的啮合周期为由齿根位置P 点进入啮合到齿顶位置N点退出啮合，其中，进入啮合区由P 点到接触线1和退出啮合区由接触线2 到N 点间的啮合位置由于边缘接触而出现应力集中，故本文中选取接触线1到接触线2 间的5 个啮合位置进行加载接触分析，获得其最大接触应力，并将其与基于赫兹接触理论的解析式(7)[12-13] 进行对比(表2)[14]，验证了有限元模型的准确性。

　　表2 单齿对模型接触应力计算结果比较

　　式中，P₀ 为最大接触应力;P 为齿面所受法向载荷;E 为弹性模量;R 为综合曲率半径;L 为接触线长度。考虑到轮齿动态接触分析存在3对齿同时啮合的情况，故本文中选取斜齿锥齿轮7齿对有限元模型进行加载啮合接触分析，装配模型如图6所示。齿轮材料选用45 钢，弹性模量为206 GP，泊松比为0.3，大轮施加的负载转矩分别为200 N·m和500 N·m。

　　3 啮合特性分析

　　3.1 齿面接触应力与齿根弯曲应力

　　通过7齿对的有限元分析，获得的整个模型的接触应力及最大弯曲应力云图如图7 所示。图7(a)所示为某瞬时3齿接触应力云图，可以看出，中间齿接触线较长且无边缘接触，另外两齿则由于边缘接触而出现应力集中。通常，Mise 应力可作为通用的应力计算准则，但斜齿锥齿轮啮合时，小轮齿面接触区域距离齿根过渡曲面较近，因而，Mise 接触应力会影响齿根处的应力分布[15]，故选用最大主应力来表征齿根过渡曲面的弯曲强度。图7(b)和图7(c)所示分别为负载500 N·m 时大轮和小轮的最大主应力云图，由图中可知，大轮的最大弯曲应力出现在靠近轮齿大端齿根过渡曲面附近，小轮的最大弯曲应力出现在靠近轮齿小端齿根过渡曲面附近。

　　为了直观反映斜齿锥齿轮的啮合特性，提取各啮合位置的最大齿面接触应力和齿根弯曲应力，其与小轮转角相关的应力变化曲线分别如图8和图9 所示。图8 中的接触应力曲线中，边缘接触区间较大，而正常啮合区间较小，这是因为斜齿锥齿轮副进入和退出啮合是一个缓慢过渡的过程。从大轮接触应力云图7(a)中可见，齿对在进入啮合区间，大轮齿顶与小轮齿根边缘接触，使得小轮齿根过渡曲面附近的接触应力较大;在正常啮合区间，在图5中接触线2 位置附近达到接触应力最大值;在退出啮合区间，小轮齿顶与大轮齿根边缘接触，使得小轮齿顶处接触应力较大。由图8中还可以看出，两种负载下的接触应力曲线变化趋势和边缘接触区基本相同，这是因为负载大小并未改变齿轮副接触线的分布和接触线的长度，这与点接触的弧齿锥齿轮副有所不同[8]71-72。

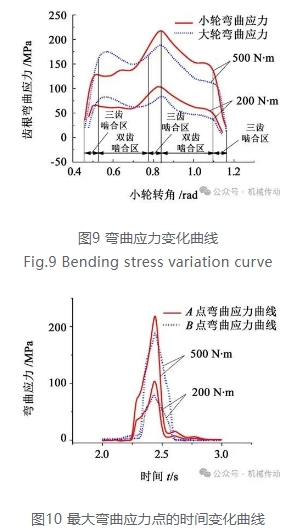
　　图9 所示弯曲应力变化曲线中，在进入啮合区间，大轮小端接触线距离齿根的高度远大于小轮，所以，大轮弯曲应力大于小轮;同理，在退出啮合区间，小轮大端接触线距离齿根的高度远大于大轮，所以，小轮弯曲应力高于大轮。由图9 中还可以看出，当大轮小端齿顶进入啮合时，出现了一个弯曲应力极值点，另一个弯曲应力极值点出现在双齿啮合最高点位置，即图7(b)中的A 点处;而小轮是小端齿根进入啮合，其唯一的弯曲应力极值点出现在双齿啮合最高位置，即图7(c)中的B 点处。图10 所示为弯曲应力云图中点A 和点B 的时间历程曲线，可以看出，点A 和点B 在啮合周期内只存在1 个峰值，且几乎出现在同一啮合位置。

　　3.2 齿面法向接触力

　　斜齿锥齿轮齿廓曲面的名义法向接触力Fn可在大轮齿宽中点的分度圆处分解为切向力Ft 、径向力Fr 和轴向力Fa 共3个分量，根据直齿锥齿轮法向接触力的解析式，斜齿锥齿轮法向接触力的表达式为

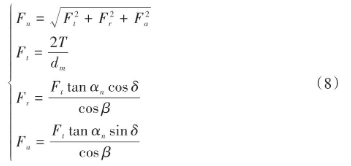
　　式中，T 为施加的负载转矩;d_m 为大轮齿宽中点分度圆直径;α_n 为法向压力角;δ 为大轮节锥角;β 为齿宽中点的螺旋角。

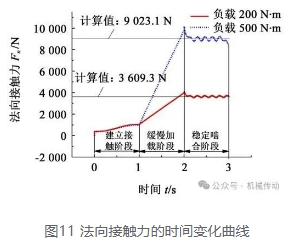
　　通过设置大轮负载转矩得到的整个模型法向接触力变化曲线如图11所示。由图11可知，接触力的变化过程包括：建立接触阶段、缓慢加载阶段和稳定啮合阶段，分别对应有限元模型前处理中的3个分析步。根据式(8)计算可得，负载转矩为200 N·m和500 N·m 时，接触力计算值分别为3 609.2 N 和9 023.1 N。在稳定啮合阶段，由于轮齿不断进入和退出啮合，接触力呈现小范围的上下波动，其中，负载转矩越大，对应接触力波动值就越大，最大波动值分别为149.6 N和-247.3 N。

　　3.3 轮对重合度

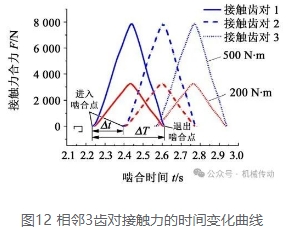
　　根据文献[16]和文献[17]中的齿轮重合度计算方法，通过测量单齿对参与啮合的时间ΔT 和相邻两齿对进入啮合的时间差Δt，则重合度为

　　将接触齿对接触力的时间历程输出，进一步得到中间相邻3 对轮齿接触力时间历程曲线如图12 所示，由式(9)计算可得，当负载分别为200 N·m 和500 N·m 时的轮对重合度分别为2.313 和2.375。从图12 中可知，斜齿锥齿轮接触力曲线较为平滑，在3 齿啮合区附近呈近对称分布，且具有较高的重合度，满足齿轮传动平稳性的必要条件。

　　4 结论

　　推导了等变位斜齿锥齿轮齿面数学模型及齿轮副接触线方程，建立了斜齿锥齿轮有限元动态接触分析模型，研究了斜齿锥齿轮的啮合特性。主要结论如下：

　　(1)齿对进入啮合时，大轮齿顶发生边缘接触，使得小轮齿根过渡曲面附近接触应力值较大;齿对退出啮合时，小轮齿顶发生边缘接触，使得小轮齿顶处应力值较大;整体来看，小轮在进入啮合时的齿面接触应力值大于退出啮合时的齿面接触应力值。

　　(2)大轮和小轮的弯曲应力极值点都发生在轮齿退出啮合时的双齿啮合最高点附近，大轮的最大弯曲应力出现在靠近大端的齿根过渡圆角处，小轮的最大弯曲应力出现在靠近小端的齿根过渡圆角处。

　　(3)斜齿锥齿轮副加载啮合过程中，在稳定啮合阶段，接触力时间历程曲线在理论计算值附近上下波动，其中，负载越大对应波动值也越大;同时，验证了计算结果与有限元分析结果的一致性。

　　(4)斜齿锥齿轮单齿接触力曲线较为平滑，在3齿啮合区附近呈近对称分布，且具有较高的重合度，满足齿轮传动平稳性的必要条件。研究结果为斜齿锥齿轮的进一步拓扑修形和性能优化奠定了基础。